Auf dem Durchgang quer durch die Rasenfläche von den Ingenieurinstituten zum großen Hörsaal und zur Informatik liegen große betonierte Halbkugeln im Weg.
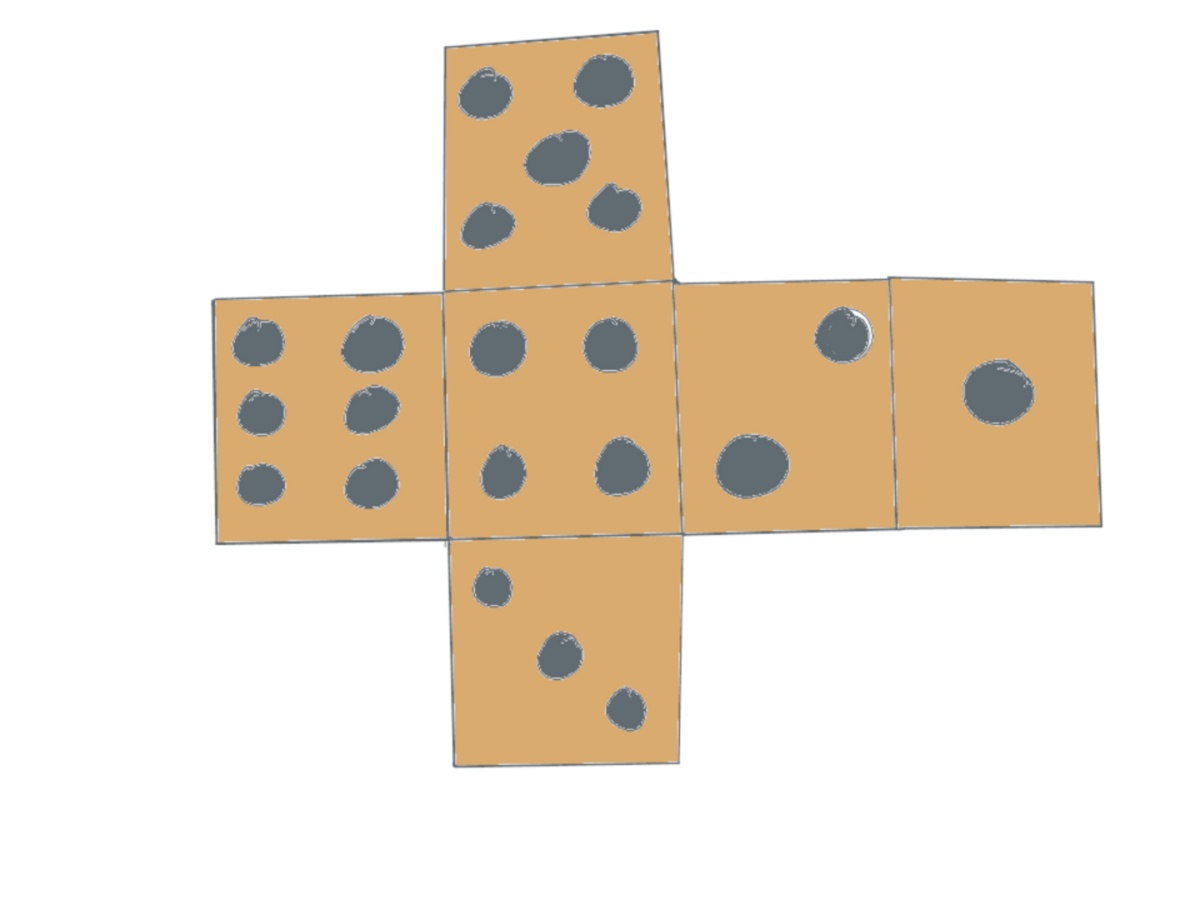
Diese sind wie die Augen auf den Seiten eines Würfels angeordnet, dabei ist die Oberfläche aufgeklappt zu einem Würfelnetz, wie man es von Bastelanleitungen her kennt.
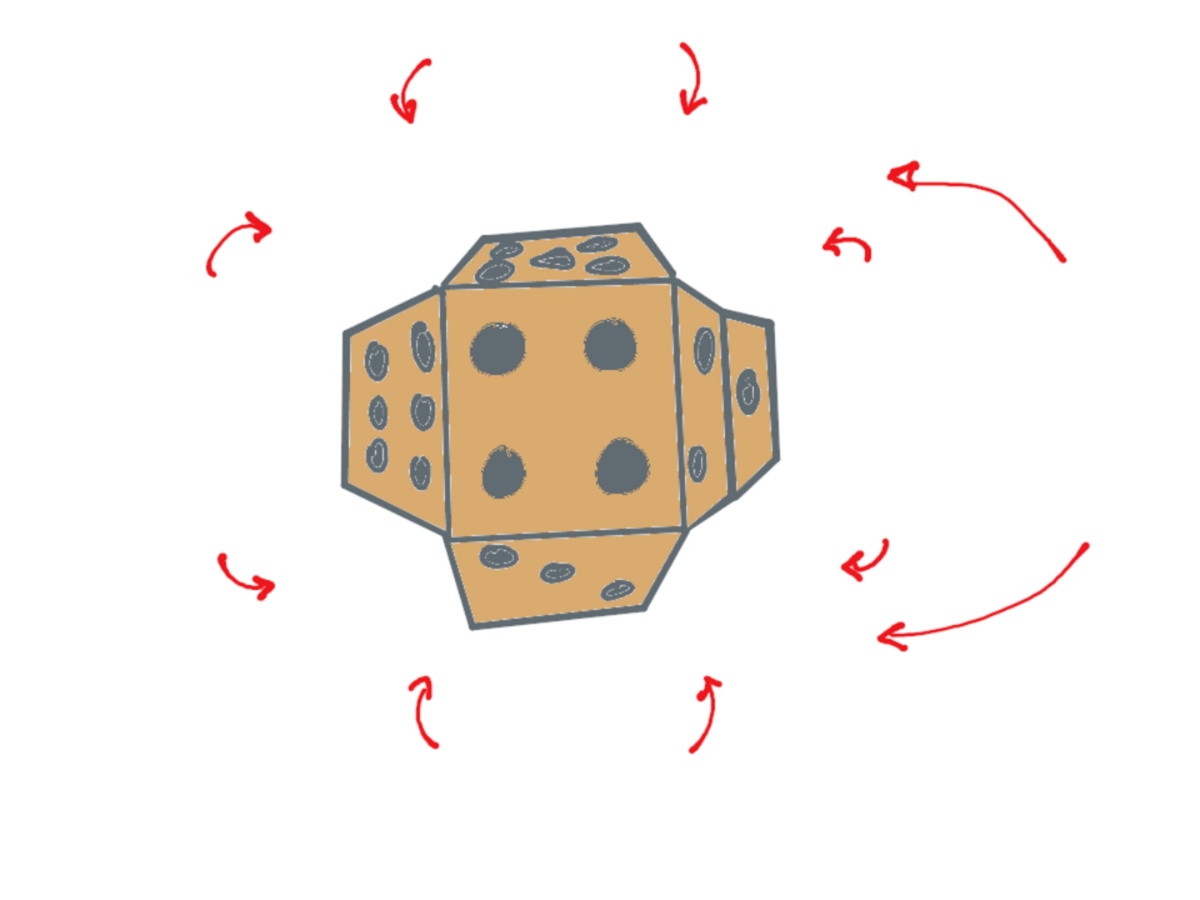
🧒 Die Bildfolge zeigt, wie der Würfel aus seinem Netz gefaltet wird.
Wer selbst Würfel aus Netzen basteln will, findet Vorlagen dazu hier als PDF-Datei.
Die Würfelaugen findet man (nur noch unvollständig erhalten) auch noch einmal in der Wiese; sie bilden dort das Würfelbeet. Im Originalzustand waren im Würfelbeet würzige Kräuter gepflanzt.
Außerdem tauchen die Würfelaugen in anderer Gestaltung noch einmal auf zwischen Mensa und Pfaffenwaldring 57 (auf dem Weg zum Teich, nicht mehr in unserem Rundgang).
Wenn man von den Würfelaugen weiter über den zentralen Platz geht, betritt man das Wegkreuz als Kreuzweg: Hier ist ein (stilisiertes) dreidimensionales Kreuz durch eine Parallelprojektion (wie beim Mosaik der Leerstühle) in der Ebene dargestellt, auf der man wandelt.
Hintergrund (mathematisch, historisch, archäologisch)
Im Würfelnetz der Lernstraße sind die Augenzahlen anders angeordnet als auf modernen Würfeln üblich.
Während sich bei handelsüblichen Würfeln gegenüberliegende Würfelseiten immer zu 7 summieren (1+6=2+5=3+4), liegen sich hier (nach dem Zusammenfalten) 1 mit 4, dann 2 mit 6, und schließlich 3 mit 5 gegenüber.
Diese Anordnung kam wohl dadurch zustande, dass im Würfelnetz die Zahlen verteilt wurden wie bei einem Hüpfspiel (den Riesen, die hier in verwunschenen Nächten hüpfen, möchten wir aber lieber nicht unter die Sohle geraten).
Es gibt (bis auf Drehung des Würfels) insgesamt 30 Möglichkeiten, die Augenzahlen auf die Seiten zu verteilen.Es gibt nämlich 6! = 6·5·4·3·2 = 720 Möglichkeiten, die Augenzahlen irgendwie auf die sechs Seiten zu verteilen, wenn der Würfel fest vor einem liegt. Da es aber 6·4= 24 = 4·3·2 Drehungen gibt, die den Würfel wieder in sich überführen, bleiben 720/24 = 6·5 = 30 Verteilungen bis auf Drehung.
Die Regel, dass sich gegenüberliegende Augenzahlen stets zu 7 addieren, stellt also eine sehr spezielle Wahl dar. Diese Regel ist schon seit mehr als 2000 Jahren nachweisbar.
Archäologisch-historische Untersuchungen von H.C. Küchelmann zeigen, dass es im alten Ägypten (vor mehr als 3000 Jahren) noch keine festgelegte Verteilung gab. Im antiken Griechenland ist die Regel dann sowohl in archäologischen Funden als auch literarisch nachweisbar. Anscheinend haben römische Soldaten im gesamten römischen Reich Würfel verbreitet, die dieser Regel folgen. Nach dem Abzug der Römer aus den Niederlanden gab es dort für einige Zeit mehr Würfel, die einer anderen Regel folgen: nämlich 1 gegenüber 2, dann 3 gegenüber 4, und schließlich 5 gegenüber 6.
Die ernsthafte historisch-archäologische Forschungsarbeit zur Verteilung der Augenzahlen auf Würfeln findet man bei
Hans Christian Küchelmann: Why 7? Rules and exceptions in the numbering of dice. Palaeohistoria 59/60 (2017/2018), 109-133.
Jelmer W. Eerkens, Alex de Voogt: The Evolution of Cubic Dice from the Roman through Post-Medieval Period in the Netherlands. Acta Archaeologica 88(1) 2017, 163-173.
Spiegelbilder
Durch die Regel gegenüber liegende Augenzahlen addieren sich zu sieben
ist die Belegung der Würfelseiten noch nicht vollständig (bis auf Drehung) festgelegt:
Es gibt zwei verschiedene Anordnungen, die sich wie Spiegelbilder zu einander verhalten.
Dieses Phänomen wird mit dem Fachbegriff Chiralität bezeichnet (auf deutsch könnte man das mit Händigkeit
übersetzen). Chiralität gibt es auch bei Molekülen, insbesondere bei Enzymen spielt diese Eigenschaft oft eine wichtige biochemische Rolle.
Bei Schraubverbindungen für Gas- bzw. Wasserleitungen wird durch Chiralität verhindert, dass versehentlich die falschen Leitungen verbunden werden.
Chiralität: Eine Spiegelung erzeugt den linken aus dem rechten Würfel (und den rechten aus dem linken).
Bei den unten gezeigten Würfeln kommt eine der beiden chiralen Versionen statistisch häufiger vor: eine Reihe tanzt aus der Reihe - welche?
